Hello,
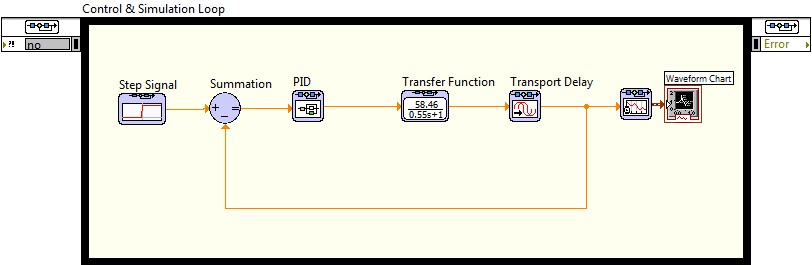
I am attempting to model the transfers of two close loop systems. They are both using direct syntheses controllers but one has deadtime compensation (smith predictor arrangement). The system which is using the dt compensation appears to yield a response which is almost identical to the desired response from which the controller was designed. However I would like to recover the transfer function from the step response such that I can properly confirm this and also compare performance characteristics and gain margin between the two systems.
So far I have been unable to recover the correct transfer function. I believe the issue may be in how the data sets are being presented to the SI Estimate Transfer Function Model VI. I have been failing with this for three days now and I have looked at most of the system identification examples. I notice that many of the examples utalize a different ODE solver, however when I have changed from the default Runge Kutta 23 it appears to distort the response. I would appreciate if someone more competent with lab view could lead me the right direction.
The desired response for the dt compensate system should be approximately;
num = [10]
den = [1, 11.2, 13.05, 10]
with 5.5 seconds deadtime
The second system without compensation should be similar but with a longer settling time and larger overshoot.
Thankyou for your help in advance.
Dan
