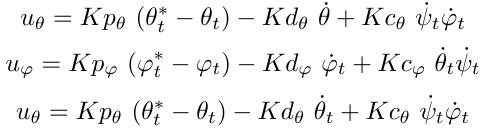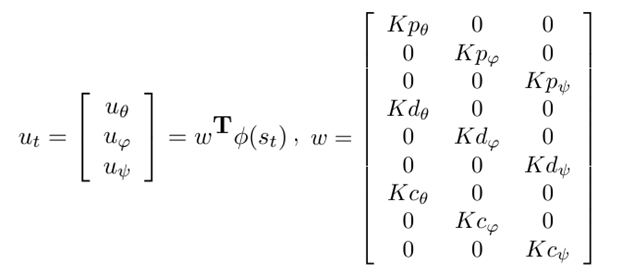Student Projects
Contact Information
University: Shanghai Jiao Tong University SJTU（East China Region）thanks to AFE Fucheng Li
Team Members: Zhang Yi(2016), Jiao Ziyuan(2016), Shen Junjie(2016)
Faculty Adviser: Assistant Professor. Ma Chenbin
Email Address: ignescent@sjtu.edu.cn
Submission Language: English
Project Information
Title: Autonomous Quad-rotor Attitude Control using Reinforcement Learning
Description
Quadrotor is a type of Unmanned Mini Aerial Vehicle, which is a nonlinear coupling dynamics system and therefore hard to control. We apply state-of- art machine learning techniques control problem of quadrotor attitude stabilization. Based on NI myRIO’s powerful computational capability and extreme portability, this algorithm is implemented as a model-free, online controller tuning procedure, which improves the controller performance, requiring no detail about the dynamical model of the vehicle.
Products
NI Hardware: NI myRIO-1900
NI Software: LabVIEW2013,
myRIO module
Real-Time module
FPGA module
MathScript RT module
Other Hardware: InvenSense MPU 9150 9-Axis Sensor
Sunnysky V2216 KV900
SkyWalker Quattro ESC
SHARP IR Sensor (GP2Y0A02YK0F)
XBee 1mW Wire Antenna Zigbee
Other Software: Matlab R2014a
The Challenge
In spite of the advantage of the flexible maneuverability, quadrotor is a dynamically unstable, nonlinear, strongly coupled system that has to be stabilized by a elaborately designed or tuned control system.
Traditionally, quadrotor applications use manually tuned PID or LQR controllers derived from a simplified linear model. These controllers require exhausting parameter identification and provide no guarantee for stability while tracking aggressive paths, especially in face of sensor noise, nonlinear disturbance and inaccurate model.
The Solution
This paper applies a state-of-art reinforcement learning algorithm called Policy Gradient via Signed Derivative (PGSD) to the control problem of quad-rotor attitude stabilization. Based on NI myRIO’s powerful computational capability and extreme portability, this algorithm is implemented as a model-free, online controller tuning procedure, which improves the controller performance, requiring no detail about the dynamical model of the vehicle. This proves to be a both adaptive and optimal control strategy, greatly overcoming nonlinearity, modeling error, environmental variants. Experiments on both simulation and hardware display the validity of the solution.
1. Controller Parametrization
In spite of strongly coupled dynamics, controller policy of a quad-rotor can be roughly separated into three less dependent channels, namely the pitch, roll and yaw channels.
We consider a linear controller with coupling term involved so that control inputs for each channel are represented as
where the angles with asterisks are the target we want to achieve at each time step.
Note that this controller parametrization is actually a strengthened PID control scheme, which also takes the nonlinear coupling terms into account. The addition of coupling terms can be proved to make the controller stable not only around equilibrium point.
In matrix form, the controller policy can be simplified as
The nine controller parameters remain to be tuned. Instead of exhaustively determining their value by manual trails or heuristics, we adopt the machine learning algorithm to automatically tune their values, based on the data collected during flight. The controller is guaranteed to converge to an optimal one after a few iterations.
2. Auto-Tuing using Reinforcement Learning Algorithm
In this section we briefly describe the reinforcement learning algorithm which runs online on NI myRIO-1900, which improves controller performance during flight. The powerful computation capability of NI myRIO-1900 makes the online execution possible with little extra effort.
Following the controller parametrization above, we consider a control cost induced by deviation from the target state at each discrete time step.
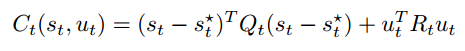
The weighting matrices Q and R are selected to be semi-definite so that the furthe the quad-rotor deviates the target state, the more cost is induced at the time step.
Consider a control task for the quad-rotor to following a series of attitude states
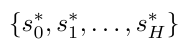
The total cost, which is the sum of all costs at each time step, is the criterion of the controller performance. Hence our aim now becomes to find a appropriate parameter matrix such that
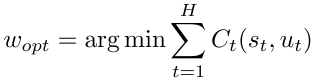
where the state and control data s and u are all derived from the flight data. This problem setting is actually a abbreviation of Markov Decision Process(MDP).
The procedure of calculating the optimal parameter matrix is based on the gradient descent method, and uses no details about dynamics model of the quad-rotor at all.
Note that in the algorithm a signed derivative matrix is still needed. This matrix can be viewd as a very rough approximation to the Jacobian matrix of the derivative of future state with respect to current control input, with the signs retained but concrete values discarded. Hence, encoded in this matrix is a rough, naive model description, which is sufficient for the algorithm to converge efficiently. In the application of our quad-rotor, the signed derivative matrix is set to
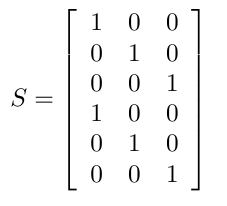
3. Hardware Experiment
NI myRIO-1900 is used as flight control processor, responsible for sensor data acquisition, data fusion, algorithm computation, rotor control as well as communication. The huge number of channels on NI myRIO and their reconfigurability make it possible to integrate multiple sensors, needed on a quad-rotor, into a unit processing center.
As the default development environment for NI myRIO, NI LabVIEW2013 provides our team with a variety of customized functionalities, extremely simplifying the development and commissioning process and allowing us to focus consistently on the high level design of the project.
In order to display the efficiency of this algorithm, we set the control loop frequency to a medium level, 100 Hz, which is commonly used on commercial quad-rotor, although myRIO FPGA allows much higher frequency.
The procedure of the experiment is as follows. At first, we choose a reasonable but not possibly optimal set of controller parameters, for instance,
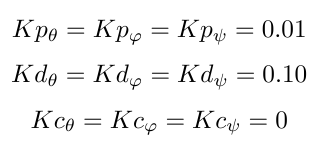
Then, we collect data while the quad-rotor is aviating for each 10 seconds, which is equivalent to H=10*100=1000 time steps. Based on the data collected, the algorithm described in section 2 updates the controller parameters automatically. This data-acquisition, update iteration runs for a few times. According to our result, 10 iteration would be sufficient for apparent improvement on controller performance to be seen.
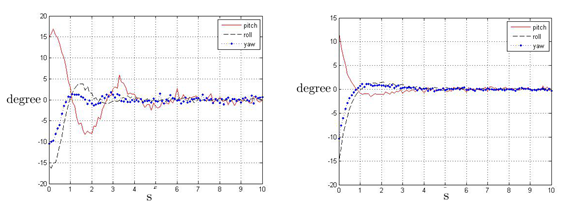
Initial performance Ultimate performance
Level of Completion: Alpha
Time to Build: Two Months
Additional revisions that could be made:
- 1. The linear controller parametrization could be replaced by a nonlinear one, for example, artificial neural network.
- 2. The Controller VI could be programmed into FPGA to release RT resource and improve performance.
- 3. Position control of the quad-rotor could be added.
- 4. The VI user interface could be strengthened.
