- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- « Previous
- Next »
How can I remove repeated elements in an array
11-07-2013 12:13 PM - edited 11-07-2013 12:26 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I'm a little late to the party, but there's always the Unique Numbers and Multiplicity VI. It may not be the fastest with regards to execution, but it's definitely the fastest to use! Particularly when it comes to documentation- heh.
Edit- quick test on my machine using Altenbach's benchmarking VI has it pretty middle-of the pack for "mostly unique" arrays, looks like it's using a search-and-build algorithm similar to Apok's suggestion. This does put it in the lead for "mostly similar" arrays though, presumably because the array that's being searched doesn't get particularly large.
This had me thinking, though- could this be done without using the search or sort functions? I put this together, and it suffers a lot for "mostly unique" or spread-out arrays, but it's actually a decent amount faster for mixed and mostly similar arrays (for positive integers) for up to about <array size>^5 (98% unique) in Altenbach's VI. I'm pretty sure the limitation is coming from the unknown array size at the end as well as the use of the max/min function, but I've not looked at it too closely yet.
Edit again- I realized that the slowdown for extremely spread-out numbers is probably because the size of the allocated Boolean array scales (more or less) linearly with the spread of the search group, making the allocation at the beginning and conversion at the end that much more expensive.
Regards,
11-07-2013 12:39 PM - edited 11-07-2013 12:50 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Great. I knew there was some slack left. 😄
Yes, it performs poorly under certain conditions. It also would not work for e.g. DBL arrays or arrays containing negative numbers, so it is not very universal.
(Now we just need to wait for a version that uses variant attributes. :D)
11-07-2013 02:13 PM - edited 11-07-2013 02:54 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
0utlaw wrote:
On Windows 2013, you can get about 30% faster than your code by not using the conditional tunnel and applying some other tweaks.. On windows 2012, the difference is probably even more dramatic.(not tested).
A quick test using variant attributes shows the speed similar to ouadji's code, so that's not a real contender.
11-07-2013 03:25 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@ouadji wrote:
altenbach's method slightly improved, slightly faster (altenbach_2)
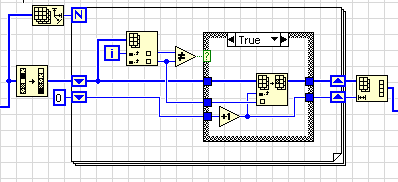
No, this code is faulty! If all elements are negative and the sorted array contains a single zero at the end, that zero is discarded in error. Try it. 😉
11-07-2013 03:32 PM - edited 11-07-2013 03:34 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
A quick recap showing how to improve outlaw's limited version (LV 2013).
(Note that "altenbach" and "ouadji II" are indistiguishable here)
(I also show a simple draft using variant attributes that can probably be improved):

11-07-2013 03:47 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach : No, this code is faulty! If all elements are ...
yes, you're right, nice shot ![]() I have already fixed this problem.
I have already fixed this problem.
11-07-2013 04:42 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
So, I went ahead and modified Altenbach's improved Boolean traverse version so that it could parse negative integers as well; it's getting a bit Rube-ish, but go figure it actually got faster again (looks like about 20-40% on my machine) for some reason. This time I'm not sure why- perhaps I'm avoiding a run-time copy of some sort by using the case structures? Ideas?
The false cases are just wired through- otherwise we shift the array so everything's positive and then un-shift it at the end.
11-07-2013 05:12 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
It does not quite make sense that it should be faster, because it does basically the same thing (actually a little bit more ;)). But, oh well, that's the LabVIEW compiler. 😄 You should also make the new value default for the "Code" array control.
It is curious that the IPE is slower than "replace array subset". I guess it does a little bit more because it also has an inner output.
You can probably remove the case structure and do the adding/subtracting irrespectively. The penalty is not measurable, but we gain speed if e.g. all inputs are positive and very large, but they only cover a small range.
- « Previous
- Next »
